Hardware aware synthesis using Classiq vs transpilation

Creating an efficient quantum circuit is something that is not very easy or trivial. What if there was a nice tool to help you create efficient quantum circuits for any quantum computer without having to re-code.

Using the Classiq platform, you can easily create an efficient quantum circuit for any target quantum computer or simulator without having to change any code. This is done by using the synthesis engine inside the Classiq platform. So, what is the difference between that synthesis engine and traditional transpilation?

If you have created quantum circuits before you probably used a transpiler to make your circuit adapt to different quantum computers, so why not just use that instead of a synthesis engine? There are multiple reasons why using the Classiq platform is easier to use and will give more optimized circuits. In this blog, I will dive a bit deeper into why synthesis gives better circuits than transpilation. The example code that I will use throughout this post is the one of a quantum adder. The function of a quantum adder is to perform an addition between two quantum registers. In this demo, we will encode the integer values of 7 and 12 into two quantum registers and save the addition result in a register called result.

Ease of programming

Let's see how to program this using the Classiq platform; this example uses the Python library of Classiq version 0.39.
The code is below, let's see what happens line by line. First, the main function is defined with 3 quantum numbers (QNum), the two numbers that will be added together, and the result.
Next, the integer values 7 and 12 are encoded in these QNum's using the prepare_int() function.
Finally, using the |= command, the result of the right side of the equation (the addition of a and b) is stored in the res QNum.

using the synthesize() method, this high-level description is turned into a quantum circuit. If you want to interactively explore the circuit, this can be done with the final show() function.

Before diving into the results. Did you see how easy that was?

from classiq import *

@qfunc
def main(a: Output[QNum], b: Output[QNum], result: Output[QNum]):
    prepare_int(7,a)
    prepare_int(12,b)
    result |= a+b

qprog = synthesize(create_model(main))
show(qprog)

Hardware aware synthesis

Now that we have a circuit, it can be transpiled to any hardware target. Let's use Qiskit to transpile this circuit to IBM Kyoto machine. The optimal transpilation gives a circuit with 366 depth, which is probably too deep to execute on any real hardware. If we want to optimize this circuit, we might want to look at different ways of implementing the + arithmetic. This is possible to do manually for such a small circuit, but it might be too hard when the circuit gets bigger. There should be a better solution right?

Luckily there is! This is where Classiq comes in. Let's use Classiq to implement the same code but optimize for the IBM Kyoto machine. It is not necessary to change the functional code that was already written. You just need to add the target machine as a back end provider, as you see in the code below. Next to the target, an optimisation parameter is also set. In this case, the circuit is optimised for depth, giving us the shallowest possible circuit for that specific machine.

from classiq import *

@qfunc
def main(a: Output[QNum], b: Output[QNum], result: Output[QNum]):
    prepare_int(7,a)
    prepare_int(12,b)
    result |= a+b

model_IBM = create_model(main)

constraints = Constraints(
    optimization_parameter=OptimizationParameter.DEPTH,
)

preferences = Preferences(
    backend_service_provider="IBM Quantum", backend_name="ibm_kyoto"
)
model_IBM = set_preferences(model_IBM, preferences)
model_IBM = set_constraints(model_IBM, constraints=constraints)

qprog_IBM = synthesize(model_IBM)
show(qprog_IBM)

When we run this code, the actual circuit that is created will be completely different. In this case, the Classiq synthesis engine picks a different implementation for the addition between the a and b variables; this new implementation is more efficient for this specific hardware target. This results in a big decrease in depth from 366 to 201. So how is this possible?

Instead of using transpilation, the Classiq platform uses hardware-aware synthesis. In this process, the creation of the quantum circuit is done from a high-level code, which is called the model. This model is turned into a quantum circuit by the synthesis engine. In this process, the synthesis engine has the flexibility to pick the best implementation of the model for each target hardware. This can give a lot of benefits for the resulting circuit in terms of depth or qubits use. In the image below, you can see more graphically the difference between transpilation and synthesis.

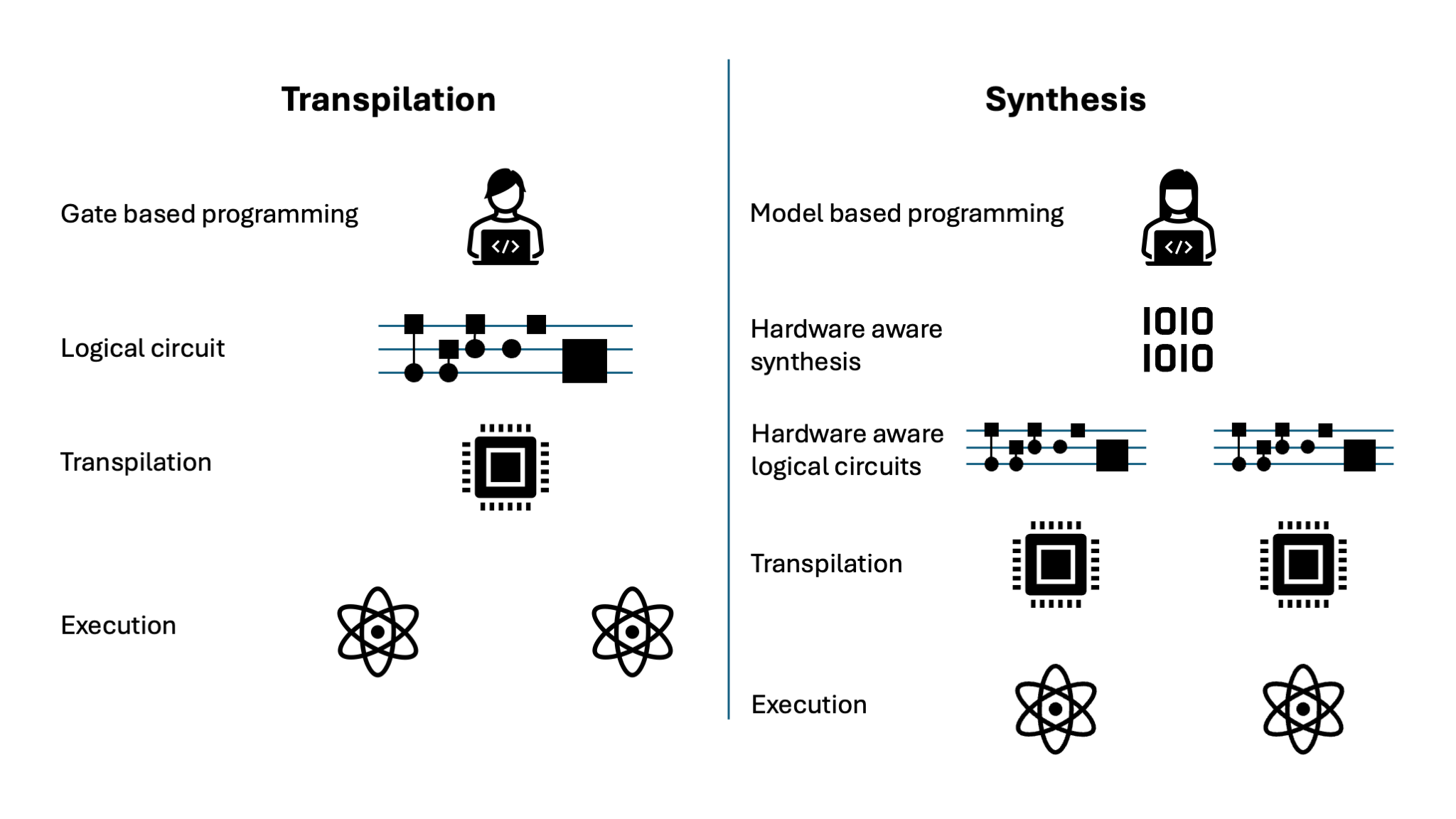
As you can see the Synthesis engine has the freedom to pick different, more efficient implementations of the same functionality. With this freedom the synthesis engine can pick the most efficient circuit implementation per hardware target. With this approach anyone can write very complex quantum circuits for any current and future quantum computer.

Recap

• With the Classiq platform, you can design quantum circuits at a high level instead of gate-based programming.
• The synthesis engine can make very efficient quantum circuits per hardware target without re-coding your quantum program.